Enhancing Result Reporting in Neuroimaging

[Gang]

Enhancing Result Reporting in Neuroimaging

--The Hidden Pitfalls of Multiple Comparison Adjustment

Gang Chen

Preface

Result reporting might seem like a mundane aspect of research, but its methodology is deeply institutionalized and often ritualized, making it almost automatic. Due to concerns about multiple comparisons, stringent thresholding has become a routine practice in neuroimaging. Any deviation from this norm is often seen as a violation of traditional standards. Reviewer 2, equipped with eagle eyes and cluster rulers, meticulously scrutinizes manuscripts, eagerly seeking those that fail to meet the stringent criteria.

In this blog post, we reexamine a crucial component of result reporting: the impact of stringent thresholding on statistical evidence. Multiple comparisons in neuroimaging remain a persistent party crasher that overstays its welcome! But is this truly a statistical faux pas, or have we simply run out of methodological munchies?

Here are our key perspectives:

1. The Current Band-Aid Approach: The current approach to handling multiple comparisons in neuroimaging is an overblown problem. Ironically, this approach contributes to reproducibility problems rather than addressing them.

2. Opportunistic or Cherry-Picking Statistical Evidence: Two different statistical metrics, family-wise error rate (FWER) and false discovery rate (FDR), are available for handling multiple comparisons. However, their adoption in practice is often based not on a consistent principle but on whichever metric presents a more favorable outcome.

3. Stringent Thresholding: The common practice of stringent thresholding harms reproducibility. The detrimental impact of this approach is evidenced by the Neuroimaging Analysis Replication and Prediction Study (NARPS). Our stance directly contradicts the conclusions drawn by NARPS.

4. Maintaining Statistical Evidence Continuity: It's crucial to maintain statistical evidence continuity in result reporting. Our recommendations, rooted in causal inference, aim to promote open science and transparency, enhance reproducibility, and challenge conventional practices.

5. Quantifying estimation: A common issue in neuroimaging result reporting is the focus solely on statistical evidence without disclosing the estimated parameter values. This practice undermines reproducibility and transparency.

6. Inefficient Modeling: The multiple comparison problem in neuroimaging can be seen as an issue of inefficient modeling. An alternative approach involves considering the data hierarchy in the modeling process. Recent developments in this area hold promise for improving modeling efficiency.

Why is stringent thresholding harmful for reproducibility?

The issue of multiplicity, or the multiple comparison problem, arising from simultaneous modeling (such as in massive univariate analysis), is generally regarded as a grave concern. The "dead salmon" episode (Bennett et al., 2010) notably triggered a knee-jerk reaction in the neuroimaging community, prompting statisticians to address the challenge. Consequently, it is considered essential to substantially discount statistical evidence at the analytical unit level (e.g., voxel, region of interest, matrix element). This is usually achieved through a penalizing process that adjusts the statistical evidence at the overall level (e.g., whole brain) by leveraging the spatial relatedness at the local level.

In common practice, there has been a strong emphasis on the stringency of result reporting, imposing an artificial dichotomization through the combination of voxel-level statistical evidence and local spatial relatedness. Various sophisticated methods have been developed to address the multiplicity issue, including random field theory, Monte Carlo simulations, and permutations. At one point, fierce competitions among these methods unfolded like a drama, vying for supremacy in the name of rigor (Eklund et al., 2016). A portion of previous publications were pinpointed and dichotomously arbitrated as failing to pass the cluster stringency funnel. Since then, an imprimatur of stringency criterion appears to have been established. Nowadays, adjusting for multiple comparisons has devolved into an oversimplified ritual. Reviewer 2 now wields newfound power and a magnifying glass to scrutinize manuscripts for any "cluster failures."

We believe there are three fundamental flaws in popular neuroimaging multiple comparison adjustments for massive univariate analysis:

(1) Faustian Bargain: Sacrificing small regions for spatial leverage.
(2) Information Waste: Ignoring valuable auxiliary information.
(3) Unrealistic Assumption: Assuming a global distribution that contradicts reality.

The Faustian Bargain: Discrimination against small regions

Traditional multiple comparison adjustments inherently penalize and overlook small brain regions based solely on their anatomical size, regardless of whether they exhibit comparable or even larger effect magnitudes. The selection of a specific threshold (e.g., threshold 1 or 2 in the figure below, Chen et al., 2020) is often considered arbitrary and raises other concerns. Apparently, smaller regions (e.g., region C) are disadvantaged relative to larger counterparts (e.g., regions A and B). The arbitrariness of threshold selection prompted the development of an alternative approach aimed at integrating spatial extent with statistical evidence strength, such as threshold-free cluster enhancement (TFCE). However, discrimination against small regions persists, as illustrated by the evaluation of region C using an integral approach (as depicted in the figure below).

Such a Faustian bargain aims to control the overall FWER, but at the cost of neglecting smaller regions. This raises a critical issue of neurological justice: Should all brain regions be treated equally in light of their effect magnitude, regardless of their anatomical size? Is this type of bias, discrimination, or sacrifice justifiable?

Information Waste: Ignoring valuable auxiliary information

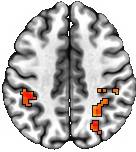
Nowadays, visual representations of results in publications are often required in a discrete and artificial manner, as exemplified below.

Two noteworthy issues arise from the figure above. Firstly, the striking cleanliness of the results may provoke skepticism regarding their alignment with real-world evidence. Could such pristine reporting practices undermine open science and transparency? Secondly, should statistical evidence alone dictate result reporting? Is there value in considering auxiliary information, such as anatomical structure or prior study results? For instance, the pronounced lack of bilateral symmetry in the figure raises a crucial question: Did the observed BOLD response truly occur asymmetrically, or does the strict adherence to artificial dichotomization, stemming from the demand by the "cluster failure" episode, create an illusion of asymmetry? Moreover, do these delineated cluster boundaries hold neurological significance?

The enduring impact of the "dead salmon" episode continues to reverberate the field to this day. It is worth questioning whether the subsequent reactions have been excessive. How "correct" and accurate are the common solutions for multiple comparison adjustment? Is the intense focus on rigor in one particular aspect causing the field to miss the forest for the trees?

An unrealistic assumption in massive univariate analysis

One problematic assumption in massive univariate analysis leads to substantial information loss. This method implicitly assumes that all analytical units (e.g., voxels, regions, correlations) are unrelated because the same model is applied simultaneously across all units. The approach assigns epistemic probabilities based on the principle of indifference (or the principle of insufficient reason), assuming a uniform distribution, where each unit can take any value with equal likelihood. In other words, the analyst assumes no prior knowledge about the distribution across the brain. In reality, the data are more likely to follow a centralized distribution, such as a Gaussian. If you are in doubt, plot a histogram of the response variable values in the brain using your own data. This will convince you whether the distribution is more accurately approximated by a uniform distribution (left below) or a centralized distribution (right below).

A statistical model should closely reflect the underlying data-generating process. The unrealistic assumption of a uniform distribution at the global level deviates from the actual data distribution, unavoidably leading to a significant loss of detection sensitivity. Common adjustment methods of controlling family-wise error rate (FWER) for multiplicity can only partially recover information loss at the local level, but not at the global level. Consequently, the excessive penalties imposed by conventional post hoc adjustment methods are like wrapping a Band-Aid around a wound—it's a superficial fix that may not be as thoroughly "correct" as the popular term multiple comparison correction implies (Chen et al., 2020; Chen et al., 2022).

Besides the excessive penalties due to the unrealistic distributional assumption, there are several other issues with the conventional multiplicity adjustment methods commonly used in practice, as elaborated in Chen et al. (2020) and Chen et al. (2022):

• Artificial and Arbitrary Dichotomy: Does statistical evidence necessarily render positive/negative dichotomy?

• Disassociation with Neurology: Do cluster boundaries carry anatomical/neurological relevance?

• Arbitrariness: The adjustment process is highly sensitive to the size and scope of the data domain, such as whether the analysis is conducted on the whole brain, gray matter, or a specific region. This flexibility introduces the risk of "adjustment hacking," where researchers might post hoc select a smaller region to apply adjustments, using techniques like small volume correction. This approach can artificially inflate the statistical evidence of results, leading to biased interpretations and diminishing the robustness of the findings.

• Ambiguity and inconsistency: Clusters often straddle multiple regions, leading to a conceptual dilemma. When a cluster only partially covers a region, can the investigator claim full involvement of that region, or must they limit their interpretation to the portion within the cluster boundaries? In practice, investigators suddenly abandon strict adherence to cluster boundaries and adopt a more stealthy strategy: they focus on identifying "peak" voxels within the clusters, then subtly extend their interpretation to include entire anatomical regions associated with those peaks, even if those regions extend beyond the cluster boundaries.

• Information Waste: A cluster is usually reduced to a single peak in result reporting and common meta-analysis.

Cherry-picking multiple comparison adjustment methods

As an alternative to spatially-leveraged FWER, the false discovery rate (FDR) is another traditional approach to handling multiplicity. Both methods share two key aspects: (1) they serve as post hoc solutions for multiplicity arising from inefficient modeling through massive univariate analysis under the assumption of uniform distribution, and (2) they discount statistical evidence without adjusting for estimation uncertainty (e.g., standard error). Compared to FWER, FDR does not discriminate against small regions. However, the less frequent use of FDR in voxel-level analysis empirically suggests its lower result survivorship in most practical applications.

In common practice, the two multiple comparison adjustment methods, FWER and FDR, are alternatives that researchers often cherry-pick based not on consistent principles but on their preferences for respective stringency. For instance, if the FDR penalty is harsher on voxel-wise results, FWER might be chosen for its consideration of local relatedness. Conversely, when FWER is not stringent enough, leading to regions of interest being overshadowed by inconveniently large surviving areas, FDR might be selected for its stricter penalty so that desirable regions could stand out. In scenarios where massive univariate analysis is performed across regions (not voxels), FDR is more likely chosen due to its more lenient penalty compared to the Bonferroni-type FWER.

NARPS as a demo case: Is result reporting a dichotomous decision-making process?

A single study cannot realistically reach a decisive conclusion. Scientific investigation has a strong cumulative element, characterized by the gradual accumulation of knowledge. Uncertainty is an intrinsic component of typical data analysis due to complex mechanisms, sample size limitations, and the stochastic nature of the underlying data-generating process. Therefore, each study should not be treated as an isolated report but rather as one of many collective efforts aimed at achieving a converging conclusion through methods like meta-analysis. It is imperative to maintain the integrity of statistical evidence in result reporting.

Do we really need cluster boundaries as a pacifier? Given the continuous nature of statistical evidence, imposing a threshold, regardless of its stringency and mathematical complexity, essentially involves drawing an arbitrary line in the sand. Clusters identified this way are as unstable as castles built in the desert. From a cognitive science perspective, this type of deterministic or black-and-white thinking through the emphasis on stringent thresholding has been described as "dichotomania" by Sander Greenland (2017) and as the "tyranny of the discontinuous mind" by Richard Dawkins (2011).

The focus on research reproducibility underscores the importance of effect estimation. The ultimate goal of scientific investigations is to understand the underlying mechanisms. From this perspective, statistical analysis should aim to assess the uncertainty of the effect under study, rather than striving for a definitive conclusion. Statistical evidence should not act as a decisive gatekeeper as in common practice, but rather play a suggestive or supporting role, helping to maintain information integrity through the uncertainty of effect estimation. Artificially dichotomizing analytical results is counterproductive and misleading, potentially creating serious reproducibility problems.

The detrimental impact of stringent thresholding, driven by excessive emphasis on multiple comparison adjustment, is exemplified by the NARPS project. The NARPS project attributed inconsistent results across teams to disparate analytical pipelines, perpetuating a "reproducibility crisis" narrative and sparking social media brouhaha reminiscent of the "dead salmon" and "cluster failure" episodes. However, contrary to the claims of the NARPS project and prevailing beliefs on social media, a more careful analysis indicates that different analytical pipelines were not the primary cause of the dramatically different results. Despite the considerable flexibility in pipeline choices, it was the enforced dichotomization through multiple comparison adjustments that largely contributed to the so-called "reproducibility crisis" (Taylor et al., 2023).

Result reporting: Can we do better?

A causal inference perspective

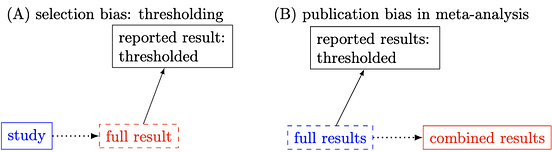
From the perspective of causal inference, the problem of stringent thresholding can be conceptualized as selection bias (left figure below). When the full result is replaced with its thresholded counterpart, comparisons with other similar studies become distorted, leading to misleading conclusions in meta-analyses (right figure below). In other words, the thresholding process is akin to conditioning on a descendant of either the response or explanatory variable. This process of conditioning on post-treatment variables introduces selection bias from a causal inference perspective. This issue mirrors the selection bias problem of "double dipping," which the neuroimaging field was fervently trying to correct around 2010. However, the same type of selection bias continues to dominate result reporting in the field.

Improving reproducibility through nuanced result reporting

Massive univariate modeling offers a conceptually straightforward and computationally feasible approach for neuroimaging data analysis. Ironically, the effort to improve reproducibility by imposing stringent multiple comparison adjustments has backfired, becoming a source of reproducibility issues itself. This pursuit of rigor through rigorous thresholding has proven counterproductive to the field.

To reduce information loss and result distortion, it is crucial to avoid artificial dichotomization through stringent thresholding. In fact, the so-called reproducibility problem, highlighted by inconsistent results across different analytical pipelines in the NARPS project, can be largely mitigated through meta-analysis using full results, as demonstrated in Taylor et al. (2023).

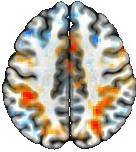
We recommend a nuanced approach to result reporting that preserves the continuum of statistical evidence. For example, apply a voxel-level threshold (e.g., p-value of 0.01) and a minimum cluster size (e.g., 20 voxels). Then, adopt a "highlight, but don't hide" method (also see the associated paper) to visually present the results, as illustrated in the figure below middle.

One may choose a particular stringency (i.e., the combination of a voxel-level threshold and a minimum cluster size) for highlighting and for addressing the multiplicity issue. While this choice might seem arbitrary, the "don't hide" aspect minimizes the arbitrariness by avoiding artificial cluster boundaries. Essentially, this method emphasizes regions with strong evidence while maintaining the continuity of information. The goal is not to make a dichotomous decision (arbitrarily labeled "valid" vs "invalid" results) but to transparently present the gradation pattern of effect patterns.

For those who prefer explicit cluster boundaries, you can still adopt your desired level of stringency (including common multiple comparison adjustment methods) and clearly mark the cluster contours, as shown in the figure above right. However, it is important to remember that such contours are not only arbitrary but also theoretically flawed, as we have argued (e.g., they can be inaccurate and discriminatory).

The benefits of our recommended result reporting are clear. Unlike the common practice of dichotomizing results (as seen in the figure above left), the "highlight, but don't hide" method offers a balanced approach that emphasizes the strength of evidence while maintaining information integrity. The illusion of asymmetry in the figure above left disappears when the full spectrum of statistical evidence is presented. Why uphold the illusion of asymmetry for the sake of an arbitrary threshold? Symmetry provides reassuring support for the presence of an effect, even if the statistical evidence doesn't meet a specific threshold. For instance, some bilaterally symmetrical regions shown in light red or blue in the middle and right figures may lack strong statistical support in this study. Yet, explicitly presenting these regions is important, as they offer potential leads for future studies. Even weaker results contribute to a broader body of evidence, potentially informing or guiding similar future studies. Transparency and open science allow everyone to make informed judgments—what harm could arise from maintaining information continuity?

Result reporting should be an engaging and thoughtful process. Instead of blindly adhering to mechanical rules (e.g., voxel-level p-value of 0.001, or a particular multiple comparison adjustment method), investigators should take a more active role. Rather than allowing statistical evidence to unilaterally dictate reporting criteria, consider the continuum of statistical evidence alongside domain-specific knowledge, including prior research and anatomical structures. This approach leads to more well-informed and robust conclusions, striking a balance between evidence strength, information integrity, and transparency. The field is gradually embracing this perspective, as evidenced by studies like a recent one published in the American Journal of Psychiatry.

Another prevalent issue in neuroimaging result reporting is the lack of effect quantification. Neuroimaging papers love flaunting t, Z, or p values with color bars and tables but rarely show actual effect magnitudes. It’s like physicists talking about the speed of light and just giving a p-value—great for keeping things mysterious! The common excuse is that parameters don’t have absolute units because the BOLD signal is relative. However, if this were truly a valid obstacle, it would imply that BOLD responses cannot be compared across individuals, conditions, and groups. If this were the case, how could a statistical model be meaningfully constructed when summarizing across individuals or comparing conditions/groups? This excuse can be easily countered by using a relative measure such as percent signal change, which is widely adopted in fMRI physics.

Scientific maturity demands a shift towards quantifying effects. The reliance on statistical values alone underscores the field's immaturity. Ignoring effect magnitudes can lead to misrepresentation and reproducibility problems. Proper scaling enables meaningful comparisons across contexts, individuals, regions, and studies, thereby supporting robust population-level analyses and meta-analyses (Chen et al., 2017). In fact, the lack of reported effect quantification was a significant issue in the NARPS project, hindering effective result summarization or meta-analysis across participating teams.

Alternative approach: Incorporating spatial hierarchy into modeling

Was the lack of stringency in multiple comparison adjustment a "cluster failure" in neuroimaging as advertised, or was it a failure to recognize data hierarchies? As the brain is an integrative organ, it would be optimal to construct a single model for each effect of interest, rather than many simultaneous models as in massive univariate analysis. Under certain circumstances, the issue of multiple comparisons can be attributed to a poor modeling approach. In these cases, the model fails to effectively capture shared information across analytical units (e.g., the brain), leading to compromised statistical inference. This scenario is particularly relevant in neuroimaging.

Indeed, directly incorporating the centralized distribution across analytical units into a single model holds strong promise. The conventional massive univariate approach treats each analytical unit as an isolated entity, leading to the multiplicity issue due to the presence of as many separate models as there are analytical units. In contrast, the hierarchical modeling approach constructs a single unified model that inherently addresses the issue of multiplicity. This method integrates multiplicity into the model itself, rather than applying it as a post hoc band-aid adjustment as seen in the traditional massive univariate analysis. In addition, brain regions are treated on an equal footing based on their respective effect strength, and smaller regions are not penalized or discriminated against due to their anatomical size.

In essence, instead of viewing multiplicity as a nuisance in massive univariate analysis that necessitates discounting statistical evidence, a hierarchical perspective transforms it into an information regularization process, enhancing the integration of statistical evidence. This hierarchical modeling approach has been implemented in the RBA program in AFNI. Due to computational constraints, it currently works with a list of brain regions instead of individual voxels. The associated theory is discussed in Chen et al. (2019). Amanda Mejia's group has also developed a similar hierarchical approach on the cortical surface.

Concluding Remarks

The issue of multiple comparisons is indeed challenging. The solution isn't simply a dichotomous choice of whether to handle multiplicity or not, but rather how to handle it effectively. Similarly, the debate on statistical thresholding has become superficial, sidestepping the deeper question: Should statistics serve as a gatekeeper or even a "guardian"?

We propose two alternatives to the current Band-Aid approach:

1. Highlight, but Don't Hide: This nuanced approach suggests emphasizing significant findings without obscuring the broader context during massive univariate analysis. This ensures transparency and maintains the integrity of the data by avoiding selective reporting.
2. Incorporating Data Hierarchies: This method integrates the inherent data hierarchies into the modeling process, providing a more robust and comprehensive analysis. By accounting for the natural structure within the data, this approach enhances the reliability and interpretability of the results.

It is worth noting that both methods avoid the cherry-picking dichotomous process between FWER and FDR.

Through this blog post, we hope to assert the following points:

• The common approaches to multiple comparisons in neuroimaging are excessively conservative. Despite significant efforts to address the multiplicity issue in massive univariate analysis over the past three decades, all current post hoc methods, regardless of their stringency, fail to account for the global distribution. This oversight results in unduly harsh penalties. Therefore, there is little justification for fixating on cluster size minutiae and voxel-level statistical evidence stringency (e.g., p-value of 0.001) as is typical in current practice.

• Arbitrary selection of methods for multiple comparisons leads to cherry-picking. Despite being different metrics, both FWER and FDR are commonly used in neuroimaging. Researchers often choose between them based on which yields more favorable results after dichotomous filtering, rather than adhering to consistent principles.

• The requirement for stringent thresholding in result reporting is damaging reproducibility in neuroimaging. The NARPS project clearly demonstrates that the detrimental impact of artificial dichotomization is a major source of the "reproducibility crisis," contrary to the dominant opinion that attributes the crisis to analytical flexibility in the field.

• Maintaining the continuous spectrum of statistical evidence is vital for achieving reproducibility. Single studies rarely achieve decisiveness in uncovering underlying mechanisms. The "highlight, but don't hide" method offers a way to preserve information integrity. Manuscripts should be evaluated holistically rather than being nitpicked for the stringency of their thresholding.

• Quantifying effects allows for improved reproducibility. A long-standing issue in neuroimaging is the neglect of effect quantification due to improper implementation in software packages. Without quantifying effects, assessing reproducibility using only statistical values is compromised.

• There is significant room for improvement in neuroimaging modeling. Massive univariate analysis has been the mainstay for the past three decades due to its straightforwardness, but its inefficiency in information calibration combined with the multiplicity challenge highlights the need for more efficient approaches. Hierarchical modeling is one small step in that direction.

P. S.

Due to the pervasive indoctrination in statistics education, for better or worse, the common practice in statistical analysis remains dominated by an obsession with p-values—a trend that may persist indefinitely. For those willing to break free from the traditional statistics doctrine and resist the alluring sirens of dichotomous thinking, thresholding, and rigid decision-making, this recent discussion by Andrew Gelman offers valuable insights.