How to Properly Select Covariates?
Gang Chen
Traditional justifications for selecting a covariate
Common reasons for including a covariate in a model often include:
- Availability: A measure was acquired and might be related to the effects under study.
- Precedence: The variable has been widely used as a covariate in previous studies or within a particularly relevant prior study.
- Intention: The investigator intends to control for a variable.
- Statistics: Metrics such as p-value and the coefficient of determination R^2 are used to gauge the importance of a variable.
These justifications are commonly cited or implicitly assumed in textbooks and the literature. The process of covariate selection is typically facilitated through model selection and comparison by adding or removing variables.
Are these justifications sound? Not really. In fact, they are neither sufficient nor necessary. One might argue that statistical evidence could be a reasonable indicator for justifying the inclusion of a covariate. However, such a justification is circular reasoning, equivalent to justifying a model based on its own output or letting the tail wag the dog. Moreover, a model's performance (e.g., R^2) only demonstrates its predictive ability (e.g., ice cream sales predicting the number of shark attacks), not its mechanistic understanding.
A model can more accurately reveal the effect of interest, but this requires that the assumptions regarding variable relationships are properly reflected in the model. Effect estimation is mechanically based on two key components: the model and the dataset. While a model cannot independently justify its validity, it is also crucial to acknowledge that data are inherently amnesiac—they do not contain information about how they were generated or which variables played critical roles. Consequently, both the model and the data are inherently agnostic about variable relationships. This prior information must be intentionally provided by the analyst. In other words, model-building should not be seen as a simple, cookbook-like pipeline. Instead, the analyst needs to take a more active and involved role than is conventionally prescribed.
Below, we demonstrate the covariate selection process using a realistic neuroimaging example.
A demonstrative example
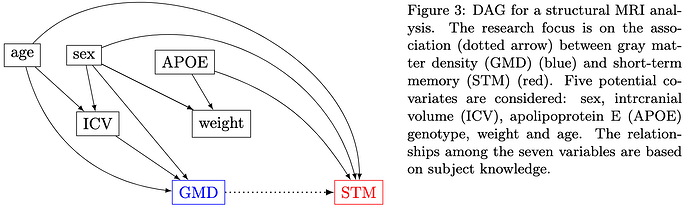
We illustrate the issue of covariate selection using a structural fMRI dataset. Suppose T1-weighted structural fMRI images are available from some participants. The goal is to investigate the impact of voxel-level gray matter density (GMD) on the behavioral measure of short-term memory (STM). In other words, GMD is the explanatory variable and STM is the response variable. Additionally, five potential covariates are under consideration: sex, age, intracranial volume (ICV), APOE genotype, and body weight.
We intend to address the following four questions:
- Explanatory Variable vs. Response Variable: While it is biologically plausible to consider GMD as a explanatory variable and STM as the response variable, conventional neuroimaging tools often assume a response variable at the voxel level. Is it justifiable, for the sake of tool convenience, to designate GMD as the response variable and STM as the explanatory variable?
- Covariates: Should all five covariates be included in the model? How does one determine which covariates should or should not be incorporated? Can the importance of a covariate or model comparisons using step-up/down procedures guide its inclusion?
- Result Interpretability/Reporting: Besides the estimated effect of GMD on STM, is it appropriate to report all other parameter estimates (e.g., sex differences in STM and the relationship between age and STM)?
- Experimental Design: Which variables could have been omitted to prevent unnecessary data collection effort and resource wastage? Alternatively, what other variables might have been included to enhance effect estimation?
By addressing these questions, we aim to clarify the principles and practices of selecting covariates, ensuring that the models we build are both meaningful and mechanistically sound.
Guiding principles in covariate selection
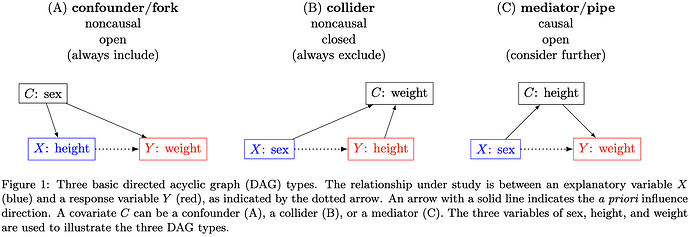
Variable relationships can be visually represented using a tool called a Directed Acyclic Graph (DAG). In a DAG, each variable is represented by a node, while the causal relationship between two variables is illustrated with an arrow (\rightarrow). Three basic relationships of a covariate (C) exist between the explanatory variable (X) and a response variable (Y): confounder, collider, and mediator.
The guiding principles for covariate selection are relatively straightforward for the first two types:
- Always include a confounder.
- Always exclude a collider.
- Handle a mediator with extreme caution.
For a mediator, the decision is a bit trickier and hinges on whether the focus is on the direct or total effect. When a mediator is present, two causal paths exist (Fig. 1C): one direct path (X\rightarrow Y) and one indirect path mediated by the covariate C (X\rightarrow C \rightarrow Y). Most of the time, the research focus is on the total causal effect of X on Y, which is the sum of both the direct and indirect paths. In this case, one should exclude the mediator C from the model. Under special circumstances where the interest is in obtaining the direct effect, the mediator should be included in the model. Additionally, partitioning mediation effects is a strong research interest, as evidenced by the popularity of mediation analysis; however, caution is needed due to its subtleties and caveats.
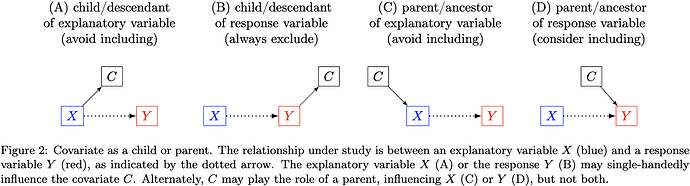
Besides these three basic types, a covariate can be a parent or child of the explanatory (or response) variable, but not both, as shown in Fig. 2 below. The principles for considering a parent/child relationship are as follows:
- Including the parent of the response variable (Fig. 2D) can help improve the precision of effect estimation.
- Do not include the covariate under all other three scenarios (Fig. 2A, B, C).
These guiding principles are rooted in their impact on effect estimation. Adhering to them can reduce potential estimation bias and improve estimation precision, while violating them may lead to biased estimates. It's crucial to emphasize two key aspects of a Directed Acyclic Graph's (DAG) role in covariate selection:
-
Embodiment of Domain Knowledge: A DAG represents one's understanding of the relationships between variables, often reflecting common background knowledge or prior information in the field. It represents the current understanding about the mechanism or the data-generating process (how the data at hand could be mechanistically produced). Even if parts of a DAG are controversial, presenting it explicitly states the investigator's assumptions. This transparency allows others to scrutinize, critique, or challenge these underlying assumptions, promoting open science and reproducibility.
-
Rule-Based Covariate Selection: By visually representing variable relationships through a DAG, one can clearly define the role each variable plays relative to the explanatory and response variables: confounder, collider, mediator, or parent/child. The decision about the inclusion or exclusion of a covariate can be justified using the aforementioned principles. When multiple DAGs are plausible, sensitivity analyses can be performed by constructing and comparing the associated models. This approach helps identify and evaluate differences in results, providing a more comprehensive understanding of the data and underlying assumptions.
By following these principles and utilizing DAGs effectively, researchers can enhance the robustness and transparency of their covariate selection process.
Revisiting the demonstrative example
Now we are ready to address the four questions raised earlier. Suppose the following DAG captures the variable relationships based on the current understanding. Applying the principles above, we can answer those questions as follows:
-
Explanatory Variable vs. Response Variable. Given that the data for GMD are at the voxel level, from a practical standpoint, it might be tempting to set STM as the explanatory variable and GMD as the response variable. However, biologically, GMD causally influences STM, not the other way around. Thus, we should choose GMD as the explanatory variable and STM as the response variable.
-
Covariates. The rationale for the decision on each of the five variables is as follows:
- Age: As a confounder, it should be included.
- Sex: As a confounder, it should be included.
- APOE: It influences STM but not GMD. As a parent of STM, its inclusion may help improve estimation precision.
- ICV: It influences GMD but not STM. Thus, it should be excluded.
- Weight: It should be excluded since it is a collider between sex and APOE. However, its inclusion might be neutral when sex, as a confounder, is considered in the model.
Based on these deliberations, we may consider the following model:
-
Result Interpretability/Reporting. In addition to the effect of interest (GMD \rightarrow STM), can one interpret and report the parameter estimation for the other three variables (age, sex, and APOE)? It is not uncommon to see such practice in the literature. However, it is important to recognize that each model is constructed for a specific relationship between the explanatory variable and the response variable. Hence, the parameter estimates for the covariates might not be appropriate due to potential bias. If the focus switches to another explanatory or response variable, the causal relationship could change (e.g., a previous confounder might become a mediator). As a result, it may be necessary to develop a new model with a revised set of covariates to effectively capture these alterations. Therefore, one should refrain from interpreting/reporting estimated parameters for those covariates unless clearly justified. In this particular example, if the focus is on the effect of age (or sex) on STM, one would build a different model in which GMD, as a mediator, would not even be included.
-
Experimental Design. Retrospectively, weight should be excluded from data collection when examining the GMD-STM relationship. On the other hand, if the number of sleep hours is deemed to have an impact on STM performance, collecting sleep data may improve estimation precision.
Summarizing remarks
Scientific investigations pivot around understanding underlying mechanisms. A statistical model, when properly built, can help reveal potentially relevant effects. However, data do not inherently keep track of their causal paths. Without appropriately incorporating prior information, a model—regardless of its performance—may not only squander crucial information but also provide misleading results. This prior information about causal relationships among variables is typically accessible through domain knowledge.
Covariate selection is a crucial component of the model-building process. It is commonly seen in the literature that the inclusion or exclusion of a covariate is based solely on "importance" measures such as p-value and the coefficient of determination R^2. Despite their intuitive appeal, such justifications for covariate selection lack a solid foundation. Instead, decisions should be rooted in principles regarding the causal relationships among the variables under consideration. Consequently, it is not surprising that some effect estimations in the literature might be biased to varying degrees. More guiding rules and derivatives can be found in Cinelli et al. (2022). For a more detailed discussion on covariate selection, refer to Chen et al. (2024).
Drawing DAGs is both rewarding and challenging. For more complex scenarios with numerous variables, graphical tools can help overcome the learning curve. For example, the R packages DAGitty and ggdag provide tools for drawing DAGs and determining the essential variables for inclusion.
Can all parameter estimates from a model be reported?
The question may sound strange at first. In the literature, it is common to see results reported for nearly all variables, including both the explanatory variable and covariates. An explanatory variable is defined as the variable of interest that impacts the response variable, while covariates are accompanying variables that are properly selected and incorporated, as discussed in here. All parameter estimates and their associated uncertainty measures can be readily obtained from the modeling process. For example, programs used in data analysis (such as 3dMVM and 3dLMEr in AFNI) allow analysts to gather any parameter estimate, regardless of whether it is an explanatory variable or a covariate, through options like -gltCode. These results are tabulated or assembled in the output (e.g., as sub-bricks).
Is there any reason that results for some variables cannot be justified in result reporting? In a straightforward experimental design with, for example, a factorial data structure, all relevant estimation such as main effects and interactions in ANOVA can all be reported with little concern. However, when covariates are involved, the differentiation between an explanatory variable and covariates becomes crucial. Each model is built to address a specific relationship between the explanatory variable and the response variable. Hence, the parameter estimates for the covariates could be biased. This is because if the focus switches to a previous covariate, the causal relationship could undergo dramatic changes (e.g., a previous confounder might become a mediator). Therefore, a different model may need to be constructed with a revised set of covariates to effectively accommodate these alterations. To summarize, it is crucial to avoid interpreting or reporting estimated parameters for covariates unless clearly justified.
Can orthogonalization be justified in modeling?
Sometime orthogonalization among variables is adopted in certain contexts, particularly when
- addressing issues like multicollinearity
- aiding result interpretation through accountability partitioning
However, such a procedure is generally not justified from a causal inference perspective because it alters the relationships among the variables, which can misrepresent the true causal structure.
First, to started with, the inclusion of all the variables in the model should be justified, as argued above. As a result, the goal is to uncover and estimate the relationships that genuinely exist among variables, as informed by a causal model (e.g., a DAG). In general a multicollinearity problem should not occur in the first place if the causal structure is properly constructed or the experiment is adequately designed.
Second, orthogonalization (e.g., via residualizing one variable against another) artificially removes shared variance between variables, potentially distorting these relationships. Specifically, orthogonalization changes what a coefficient represent:
- Without orthogonalization, a coefficient captures the direct effects of an explanatory variable, conditional on other included variables.
- After orthogonalization, a coefficient reflects the effect adjusted for a manipulated, noncausal relationship (e.g., the residuals instead of the raw variable). This adjustment can obscure the true causal interpretation of the coefficients. Instead, it may introduces bias or captures statistical artifacts rather than meaningful causal constructs.
In summary, orthogonalization is generally discouraged because it distorts the natural dependencies among variables and undermines the interpretation of causal effects. Instead, causal inference relies on explicit assumptions and causal structure to handle relationships between variables in a principled way. Orthogonalization may be justified in limited contexts, for instance, when causal interpretation is not the goal (e.g., for purely predictive purposes).