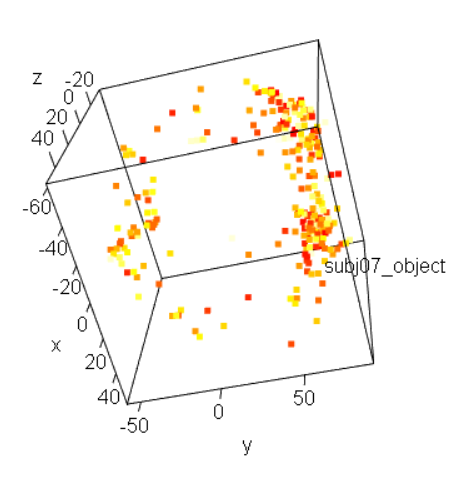
Imagine you have a 3D matrix M of dimensions (in terms of voxel counting) X, Y and Z, and you want to flatten it to a 1D-indexed vector V. There are a total T = X*Y*Z elements in both M and V, just that each element of M is accessed as M[i,j,k] and each in V is V[n], say. We want to make a 1-to-one mapping between each i,j,k triplet and a particular n.
I wrote a Python program to do this---again, my lack of R-ability! Python is 0-based, instead of 1-based like R. Also, the interval specifications in Python here are half-open: so range(0,X) means [0,X), which means 0, 1, 2,..., X-1. This is how I picture what should be done, with the two map*() functions here showing how you can go back and forth between "i,j,k" and "n" representations. Note that these functions work as a pair---if one walked through the matrix in a different ordering, then the partner mapping function would have to change.
- Another important feature to highlight is that when going from a 3D obj-> 1D one, there are 3 nested loops; when going from 1D -> 3D, there is a single loop. I didn't see any nested loops in your program.
# import module to have array types around
import numpy as np
# make matrix with some data, of size 3x4x5
M = np.random.randint(0,100, size=(3,4,5))
# obtain matrix and vector dim variables, from matrix M's dimensions
X, Y, Z = np.shape(M)
T = X*Y*Z
def map_idx_Mijk_to_Vn(i,j,k):
"""Flattening done: row-by-row and plane-by-plane:
Plane count : X*Y
Row count : X
"""
plane = X*Y
n = k*plane + j*X + i
return n
def map_idx_Vn_to_Mijk(n):
"""Un-Flattening
Plane count : X*Y
Row count : X
"""
plane = X*Y
# which plane?
k = int(n/plane)
# ... and remove the plane count
rem = n - k*plane
# which row?
j = int(rem/X)
# ... and remove the row count
i = rem - j*X
return i, j, k
# ----------------------------------------------------------------------
# use
# map matrix M (exists) to vector V (initialize with integer zeros first)
V = np.zeros(T, dtype=int)
for i in range(0,X):
for j in range(0,Y):
for k in range(0,Z):
n = map_idx_Mijk_to_Vn(i,j,k)
print(i,j,k, n)
V[n] = M[i,j,k]
# map vector V (exists) to matrix M2 (initialize with integer zeros first)
M2 = np.zeros((X,Y,Z), dtype=int)
for n in range(0,T):
i,j,k = map_idx_Vn_to_Mijk(n)
print(i,j,k, n)
M2[i,j,k] = V[n]
# -----------------------------------------
# test
# The two printed things here should be equal.
# The trio can be changed and this should work
my_x = 2
my_y = 3
my_z = 4
print(M[my_x, my_y, my_z])
my_n = map_idx_Mijk_to_Vn(my_x, my_y, my_z)
print(V[my_n])
--pt